Research

My research interests are primarily in studying moduli spaces of curves and their Chow rings. In particular I have focused on using the combinatorial description of these rings' intersection products to study families of effective classes. I am also interested in related material, such as more general moduli space theory, Gromov-Witten theory, and CohFTs.

My current specific topics of interest include the geometric interplay of different families of compactifications of moduli space of curves, as well as special tautological classes such as hyperelliptic loci and various variations of \(\psi\)-classes. I am also involved in a research group studying the connections between spaces of random polygons and moduli spaces of curves, which, via the study of Hassett spaces, has connections to tropical geometry, the combinatorics of weighted \(\psi\)-classes, and flat surfaces.

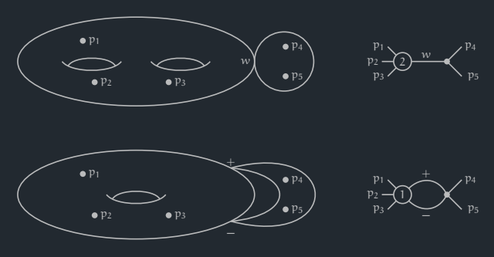
The banner page image is a slice of a (long) calculation used to build evidence for some of the conjectures proved in our paper on ω-class intersections. The image to the right is a pair of topological and dual graph representations of the general points of special tautological loci in \(\overline{\mathcal{M}}_{2,5}\) from my paper on hyperelliptic classes.

Papers and Preprints

Published

On compactifications of \(\mathcal{M}_{g,n}\) with colliding markings (with Sebastian Bozlee) (Selecta Mathematica (2024), 30, 104) [arXiv]
Extremality of rational tails boundary strata in \(\overline{\mathcal{M}}_{g,n}\) (European Journal of Mathematics (2022), 8, 523–539) [arXiv]
Witten's conjecture and recursions for \(\kappa\) classes (with Renzo Cavalieri) (European Journal of Mathematics (2021), 7, 309–339) [arXiv]
Wall-crossings for Hassett descendant potentials (with Renzo Cavalieri) (International Mathematics Research Notices (2020), doi:10.1093/imrn/rnaa077) [arXiv]
Hyperelliptic classes are rigid and extremal in genus two (Épijournal de Géométrie Algébrique, Volume 4 (2020), Article no.2) [arXiv]
Properties of tautological classes and their intersections (Dissertation, Colorado State University (2019))
Julia and Mandelbrot sets for dynamics over the hyperbolic numbers (with Tristan Rendfrey, Aaron Shukert, and Patrick Shipman) (Fractal Fract, 2019, 3(1), 6) [arXiv]
Intersections of \(\omega\) classes in \(\overline{\mathcal{M}}_{g,n}\) (with Renzo Cavalieri) (Gökova Geometry/Topology Conference Proceedings, 2017) [arXiv]

Projects in Progress

Moduli theory of the \(r\)-braid arrangement (with Emily Clader, Iva Halacheva, Haggai Liu, and Dusty Ross)
Sign reversing involutions in moduli spaces of curves (with Maria Gillespie and Jake Levinson))
Gravitational descendants of Gorenstein compactifications of \(\mathcal{M}_{1,n}\) (with Sebastian Bozlee)
Tropicalizations of moduli spaces of simplicially stable curves (with Andy Fry)

Odds and Ends

Leftovers from various projects

A poster about hyperelliptic loci, presented at WAGS in Los Angeles, CA in 2017
A Maple workbook to compute pushforwards of polynomials of \(\kappa\)-classes (written in/for Maple 2016)
An Overleaf document with occasionally useful \(\LaTeX\) things
Slides for a silly Valentine's Day talk at CSU

Vance Blankers

Home Research Teaching Life